Lab 08 -modelowanie danych: regresja
Lab 07 - Modelowanie danych
Wprowadzenie
Celem zajęć jest przedstawienie procedury budowy modelu opartego o analizę danych, który pozwala wyjaśnić relacje między nimi. Zasadniczo dla danych ciągłych model taki jest regresorem opisanym przez regresję liniową lub nieliniową.
W przykładowej analizie realizowanej w ramach wprowadzenia będzie
wykorzystywany zbiór
danych. Zawierający dane z eksperymentu obciążania belki zmienną
siłą, podczas którego rejestrowano ugięcie belki. Dane mają postać: 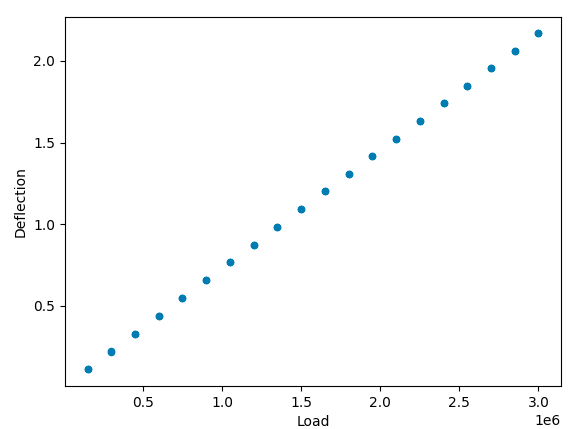
Regresja liniowa dla jednej zmiennej
Z otrzymanego wykresu możemy stwierdzić, że model opisujący zależność między obciążeniem a ugięciem jest modelem liniowym \[D_{deflection} = a \cdot X_{load} + b\]
Współczynniki takiego modelu mogą być wyznaczone przy pomocy regresji
liniowej. Do wyznaczenia regresji można użyc wielu różnych modułów:
scipy.stats.linregress,
sklearn.linear_model.LinearRegression,jednak na zajęciach
będziemy wykorzystywali funkcję
statsmodels.formula.api.ols, który dobrze integruje się z
pandas i poza wyznaczeniem współczynników modelu pozwala na
wyznaczenie również statystyk dotyczących istotności otrzymanych wyników
oraz przedziałów ufności dla parametrów.
from statsmodels.formula.api import ols
model = ols('Deflection ~ Load', data=data)
res = model.fit()
res.summary()model opisany jest w stylu języka R więcej informacji na
temat definiowania modeli, które mogą być zarówno liniowe jak
nieliniowe, obejmować zmienne kategoryczne i ciągłe, można znaleźć w dokumentacji
Efekt dopasowania można wyświetlić używając metody
predict, lub tworząc wyrażenie zawierające wyestymowane
współczynniki: data[‘Prediction’] = model.predict(data)
ax = data.plot.scatter(x=‘Load’,y=‘Deflection’, ax=axs[0,0])
Analiza wyników faza 1
wynikiem metody res.summary() jest następujący zbiór
danych: 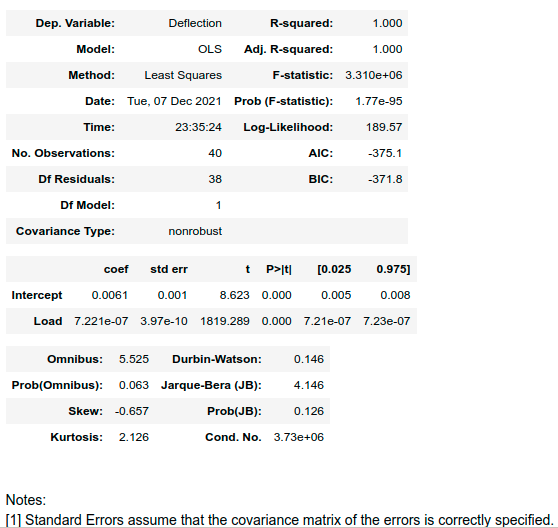
Warto zwrócić uwagę na następujące metryki: - R-squared
(R2) - współczynnik
determinacji, wyrażony jako iloraz wariancji wyników predykowanych z
modelu do wariancji wyników rzeczywistych. Jest jedną z
najpopularniejszych metryk opisujących dopasowanie modelu do danych, gdy
ma wartość 1, oznacza to bardzo dobre dopasowanie inne wartości wskazują
na rozbieżności w dopasowania, ma wartość 0, gdy model zwraca wartość
średnią. Otrzymana wartość wskazuje na bardzo dobre dopasowanie modelu
do danych. Aktualnie dokładniejszymi metrykami są AIC i BIC.
coef- kolumna zawiera wyestymowane współczynniki regresji dla obciążenia (Load) i skłądową stałą (intercept), kolejne kolumn zwiarają błąd standardowy współczynnika (std err), prawdopodobieństwo testowe (P) oraz przedział ufności dla poziomu ufności 0.95Omnibus test,Prob(Omnibus)- statystyki pozwalające określić na ile zaproponowany model jest w stanie zmniejszyć wariancję błędu (residuów). Statystyka (F-test) jest wykorzystywana w teście ANOVA i będzie omawiana na kolejnych zajęciach. Na chwilę obecną można stwierdzić, że Prob(Omnibus) wskazuje, że jest 6.3% szans że dopasowany model w pełni wyjaśnia wariancję
Mogłoby się wydawać, że otrzymane są bardzo dobre poza wynikiem testu Omnibus, który może wskazywać na to że występują inne, nieuwzględnione w modelu zależności.
import statsmodels.graphics.gofplots as sm
fig, axs = plt.subplots(2,2, squeeze=False)
data['Prediction'] = res.predict(data)
plt.tight_layout()
ax = data.plot.scatter(x='Load',y='Deflection', ax=axs[0,0])
data.plot(x='Load',y='Prediction', ax=axs[0,0], color='red')
# plt.subplot(2,2,2)
residuals = res.predict(data)-data['Deflection']
axs[0,1].scatter(data['Load'], (residuals))
axs[0,1].set_xlabel('Load')
axs[0,1].set_ylabel('Residual values')
axs[1,0].hist(residuals)
axs[1,0].set_ylabel('frequency')
axs[1,0].set_xlabel('residuual values')
plt.subplot(2,2,4)
sm.qqplot(residuals, stats.t, distargs=(4,), loc=3, scale=10, fit=True, ax=axs[1,1], line='s')
plt.tight_layout()a efektem jest wykres:
wynikiem metody res.summary() jest następujący zbiór
danych: 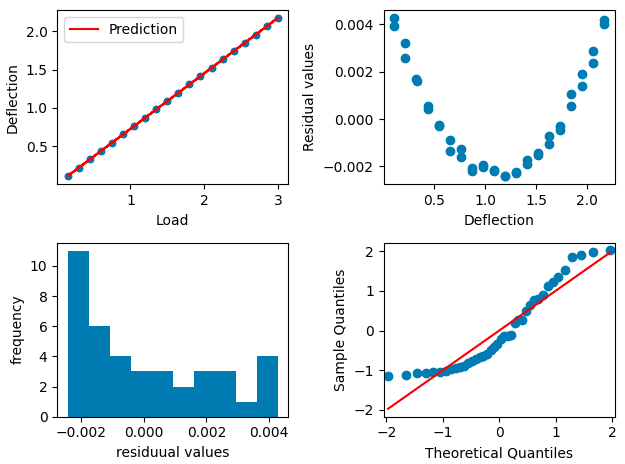
Z analizy residuów widać, że błąd dopasowania ma charakter systematyczny a nie przypadkowy, co potwierdza wynik testu Omnibus. Również histogram nie ma rozkładu normalnego, co miałoby miejsce, gdyby elementem, którego nie może wyjaśnić model jest szum biały. Z Q-Q plot można również ocenić że residuua nie mają rozkładu normalnego. ### Poprawa modelu Poprawa modelu odbywa się głównie przez analizę residuów. W tym przypadku można przypuszczać, że brakujący człon ma jest zbliżony do paraboli.
W przypadku regresji liniowej, człon wykładniczy możemy zrealizować przez dodanie kolejnej zmiennej która jest kwadratem zmiennej wejściowej:
Model będzie miał więc postać:
data['Load2'] = data['Load']**2
model = ols('Deflection ~ Load + Load2', data=data)
res = model.fit()Przeanalizuj wyniki i sprawdź jak rozszerzenie modelu wpłynęło na wartości statytsyk, wartości parametrów modelu oraz na przedział ufności poszczególnych parametrów. Szczególną uwagę zwróć na Omnibus test.
Dalsze działania
W poniższych zadaniach wykorzystaj dane z zeszłych zajęć (zbiór danych, lub alternatywny link), oraz stworzone wtedy kody służące do wczytywania i czyszczenia danych.
- Spróbuj postępując zgodnie z przedstawioną metodą wyznaczyć model
dla relacji między ceną sprzedaży nieruchomości (
SalePrice) aGrLivArea - Spróbuj postępując zgodnie z przedstawioną metodą wyznaczyć model
dla relacji między ceną sprzedaży nieruchomości (
SalePrice) aOverallQual3. - Spróbuj wyznaczyć model który jest połączeniem modelu 1 i 2 oraz
dodatkowo zawiera dane dotyczące i
TotalBsmtSF(model powinien być sumą etykiet poszczególnych kolumn) - Dla każdego modelu oceń jak zmienia się wariancji wartości residuów oraz statystyki. Czy model 3 dał istotną poprawę jakości dopasowanie, zmniejszył wariancję?
- Na podstawie własnej analizy z poprzednich zajęć wybierz 4 cechy,
które twoim zdaniem będą najlepiej reprezentowały cenę i stosując metodę
z poprzednich zajęć (las drzew) spróbuj ocenić dokładność regresji w
porównaniu z wynikami modeli 1,2,3. W tym celu wyznacz wartość R2 (do
tego celu możesz wykorzystać
from sklearn.metrics import r2_score, lub zaimplementować odpowiednie wyrażenie zgodnie ze wzorem)
Autorzy: Piotr Kaczmarek